半導体の微細化関連の最後のトピックとして、少し専門的かつ理論的なお話をしておきたいと思います。できるだけわかりやすく説明したいと思いますので、専門的な知識のない方も少しお付き合いください。
2021年07月13日 公開
2025年04月23日 更新
第7回 半導体の微細化 スケーリング則とは
デナードのスケーリング則
第1回でお話ししたムーアの法則「一つのチップ上の素子数は2年で倍増する」は経験に基づく予測でしたが、実はムーアの法則を支える理論の裏付けのある法則があります。“スケーリング則”と呼ばれるもので、IBMのデナードが1974年に学会誌の論文で発表したものです。デナード・スケーリング、デナード則、あるいは日本語で比例縮小則と呼ばれることもあります。
第4回から第6回で半導体ビジネスの歴史や半導体デバイスの発展の経緯をお話ししましたが、スケーリング則が発表された1974年は、MOS集積回路の技術が成熟しビジネスが立ち上がり、微細化が本格的に進み出した頃だったと思われます。
微細化してもトランジスタが小さくなるだけで動作原理は全く変わりませんが、スケーリング則は「小さくすることはいいことだ」ということを理論的に示しました。ただしMOSトランジスタを使ったデジタル回路に限っての話ですが。
スケーリング(Scaling)とは図形などの拡大縮小という意味で、半導体以外でもスケーリング則というものはありますが、半導体の場合は、MOSトランジスタを縮小するときの指針を示し、その指針通りに縮小した時にMOSトランジスタの特性や回路の性能がどうなるかを理論的に示したものです。
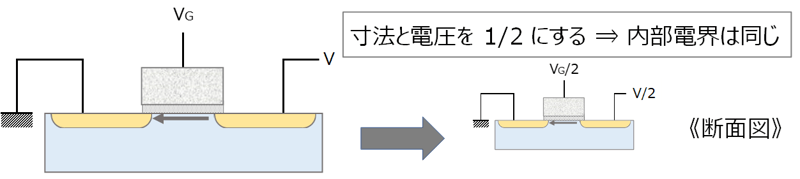
大きさを小さくしたのに印加する電圧をそのままにしておくと、デバイスがうまく動作しなかったり壊れたりしてしまうので、印加する電圧も同じ割合で小さくします。そうすると「素子の集積度は上がるが素子の消費電力は小さくなるので、チップ面積が同じなら消費電力は増加せず、しかしデジタル回路のスピードは速くなる」というデジタル回路にとっては理想的な結果になります。
以下に具体的なスケーリング則の内容を説明しますが、全てを細部まで理解できなくても、なんとなくイメージをつかんでいただくだけでもいいと思いますので、気軽に読み進んでください。
例えば1/2にスケーリングするとどうなる?
例としてMOSトランジスタを1/2倍(0.5倍)にスケーリングした時の様子を説明します。

①寸法と電圧のスケーリング
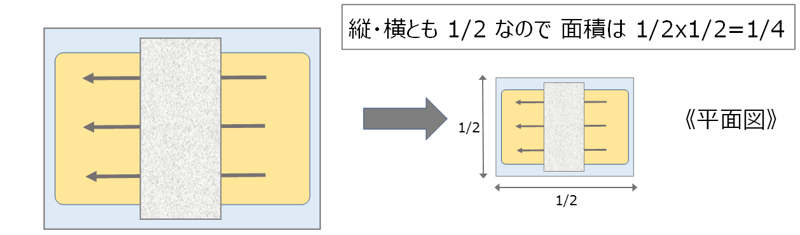
②面積のスケーリング
③電流・電圧のスケーリング
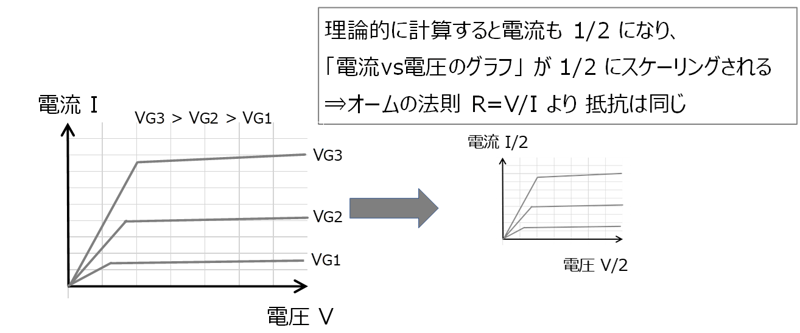
※専門的になりすぎるので詳細は述べませんが、基板不純物濃度(Siウェーハ中の不純物濃度)は2倍に増やします。不純物の添加に関しては第2回で簡単に説明しています。
④消費電力のスケーリング
②と③から消費電力に関して以下のことが言えます。
- ③に示したように電圧・電流ともに1/2にスケーリングされます。消費電力は電圧x電流なので、スケーリング後の消費電力は1/2x1/2=1/4となり「消費電力が4分の1」になります。
- ②より面積も4分の1なので「単位面積当たりの消費電力はスケーリングしても同じ」ということになります。Siチップの面積が同じなら高集積化しても消費電力は変わらないということです(下図)。
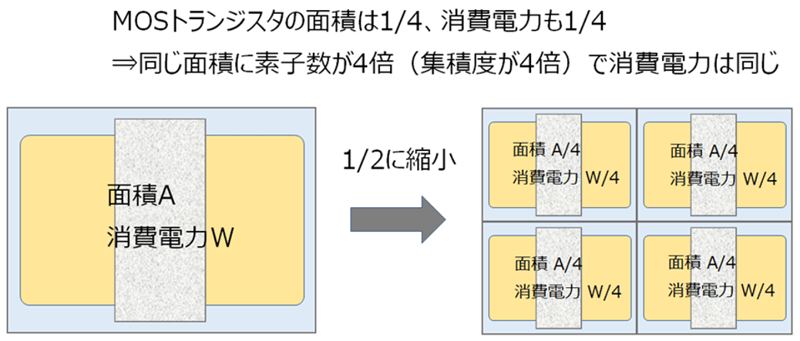
「単位面積当たりの消費電力はスケーリングしても同じ」これは非常に重要です。もしこれが成り立たず消費電力が増加したとすると、発熱量が増えて温度が上昇し、回路が動作しなくなったり壊れたりします。そうなると、微細化はできても高集積化ができず、結果としてムーアの法則が成り立たなくなります。
ここまでで、スケーリング則に則って微細化すれば消費電力を増やすことなく高集積化ができ、ムーアの法則が実現できることがわかりましたが、回路の性能はどうなるのでしょうか?
答えは「デジタル回路では高速化が実現できます」になります。小さくなるので信号が伝わる時間が短くなるような気もしますが、電流が減るのに速くなるのはおかしな気もしますね。では速くなる理由を次に説明します。
デジタル回路はなぜ高速化するのか?
上で述べたようにスケーリングすることで電流もスケーリングされて減少するのですが、デジタル回路は高速化します。
電流が減るのに高速化する?直感的に疑問に思う人もいるかもしれません。
確かに他は同じで電流だけが減れば当然遅くなりますが、デジタル回路のスピードに影響を与える電流以外の要素もスケーリングされてそちらの影響の方が大きいので速くなります。詳しく説明するには、デジタル回路がどのように信号(情報)を伝えるかを考える必要がありますので、以下に説明します。
まず専門的な言葉で簡単に説明すると、以下のようになります。
デジタル回路のスピードは次段のゲート容量Cの充放電時間Tで決まります。具体例として、もっとも簡単な回路であるNOT回路(インバーター)で出力が「0」から「1」になる場合を考えます(下図)。NOT回路1の入力が「1」から「0」に変わるとPMOSがONして電流が流れ、それによって次段のゲート容量Cが充電されて電圧が上昇し、NOT回路1の出力(=NOT回路2の入力)が「0」から「1」に変わります。
回路の出力が「0」から「1」になる時間すなわちゲート容量Cの充電時間Tは、「1」に相当する電圧をV、そのために充電すべき電荷をQ、充電電流をIとすると、コンデンサの容量の式からQ=CVなので、T=Q/I=CV/Iとなります。
1/2にスケーリングすると、VもIも1/2にスケーリングされます。またゲート容量Cも簡単な計算(文末の補足説明)で1/2にスケーリングされることがわかります。充電時間T=CV/IのC、V、Iがそれぞれ1/2になるのでTも1/2になり、すなわちスピードが2倍になることがわかります。
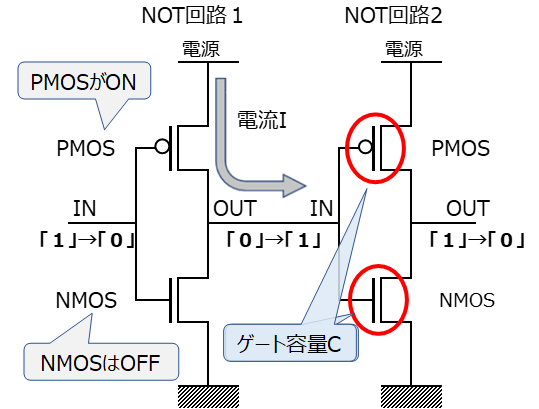
※細かいことを言うと、ゲート容量以外にも配線容量などの寄生容量も考慮する必要があります。
専門的な言葉を極力使わずに説明すると、回りくどくなりますが以下のようになります。①デジタル回路とは、②デジタル回路の動作、③微細化すると速くなるわけ、の順番で説明します。
①デジタル回路とは
デジタルの対義語はアナログです。アナログは連続量を、デジタルは離散量(とびとびの値)を意味する言葉です。例えば、アナログ時計は文字盤と針で時間を表しますが、デジタル時計は数字で時間を表示し、一般的には分単位で表示されます。1分単位のとびとびの値で表示されますので、例えば7時30分の次は7時31分です。
 アナログ時計(左)とデジタル時計(右)
アナログ時計(左)とデジタル時計(右)
デジタル回路は、定義上は離散的な値を扱う回路になりますが、ほとんどの場合は「0」と「1」というふたつの値だけを扱います。入力が1種類の場合も複数の場合もありますが、すべて「0」か「1」のどちらかです。この入力に対して何らかの処理を行い「0」と「1」で構成される情報を出力します。電気的には電圧の大小で「0」と「1」を表現しています。具体的にはゼロV付近の電圧を「0」、電源電圧付近の電圧を「1」として考えます。真と偽の二つの状態を扱う論理演算や2進数の演算はデジタル回路で表現できます。
デジタル回路を使った代表的な製品がロジック製品です。ロジック製品にも小規模なものから大規模なものまでいろいろありますが、マイクロプロセッサ(MPU)やGPUなどが代表的な最先端のロジック製品です。
※ロジック製品については第19回と第20回で詳しく説明しています。
ロジック製品内では、基本となる簡単なデジタルロジック回路の出力が次の回路の入力になり、その出力がまた次の回路の入力になり、ということを繰り返して複雑な処理を行っています。
下図に2本の入力端子を持つAND回路の例を示します。AND回路は2本の入力がどちらも「1」の場合だけ「1」を出力するので、以下の例では出力は「0」となります。CMOSのAND回路はPMOS・NMOS各3個で構成できます。
②デジタル回路の動作
「1」に相当する高い電圧を作るには電気(プラスの電荷)を溜める必要があり、「1」を「0」にするには溜めた電気を抜く必要があります。あくまでイメージですが、水に例えると、バケツ等の器に水を満杯に入れた状態が「1」、水を抜いて空にした状態が「0」、水の深さが電圧に相当する、という感じです。
デジタル回路の動作が速いというのは、電気を溜めたり抜いたりする時間が短いということです。これは電気を溜めたり抜いたりする速さ、すなわち電気の流れる速さ(電流)と溜めるべき電気の量で決まります。
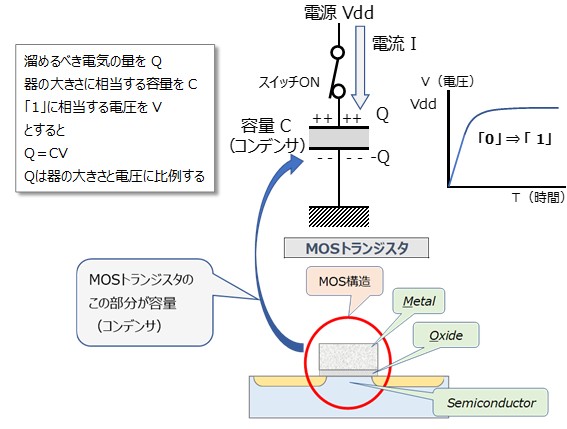
理科系の方はよくご存じのように、電気の量Qは電気を溜める器の大きさ(容量)Cと必要な電圧Vに比例し、Q=CVとなります(下図のテキストボックス参照)。
下の図は「1」に相当する高い電圧を作る場合の模式図です。容量と書いてある部分が電気を溜める器(なじみのある用語でいうとコンデンサ)になります。CMOSデジタル回路の場合は、図の中のスイッチはPMOSになります。PMOSがONして電源から電流が流れて容量に電気を溜めることで「1」を出力(=次のデジタル回路の入力)します。MOSデジタル回路の場合、次のデジタル回路の入力端子に相当するMOSトランジスタのゲート電極部分がまさにこの容量に相当します。
③微細化すると速くなるわけ
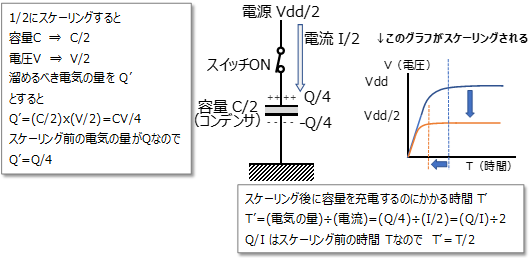
微細化(スケーリング)すると速くなるというのは、上の図の電流Iも小さくなるが、電気を溜める器の大きさ(容量)も電圧もどちらも小さくなるので、溜めるべき電気の量Qはもっと小さくなるからです。
1/2にスケーリングする場合を考えると(下図)、(文末補足説明に示したように)器の大きさ(容量C)も電圧Vもどちらも同様に1/2になります。すなわち溜めるべき電気の量Q=CVは1/2x1/2で1/4になります。「0」から「1」にするのにかかる時間は、電気の量Q÷電流Iです。1/2にスケーリングされると、電気の量が1/4、電流が1/2にそれぞれスケーリングされるので、この時間は1/4÷1/2=1/2で1/2にスケーリングされます。すなわち2倍高速になります。
以上デジタル回路については微細化(スケーリング)が大いにメリットになるということをお話ししました。
メリットを改めて整理しておくと以下になります。
①高集積(集積度一定の場合はチップ面積縮小) ②高速 ③低消費電力
※ここで説明したデジタル回路の消費電力を以下の補足説明で計算していますので、興味のある方はご覧ください。
元々はこの回が微細化シリーズの最終回のつもりだったのですが、書いているうちにどんどんボリュームが増えてしまいまして、あと2回続きます。次回は、スケーリング則のようなうまい話は永遠には続きません、というお話です。
補足説明
◯ゲート容量Cの計算(1/2にスケーリングした場合)
ゲート容量というのは②デジタル回路の動作の図の赤丸部分でコンデンサになっている。コンデンサの容量式からゲート容量Cg=εA / Tox(Aは電極面積、Toxは図のOxideの厚さ、εはOxideの誘電率)、Aは面積なので1/2x1/2=1/4にスケーリングされ厚さToxは1/2にスケーリングされるので、スケーリング後の容量は1/4÷1/2=1/2にスケーリングされる。εは物質固有の値なのでスケーリングされない。
◯デジタル回路の消費電力とスケーリング
本文で説明したように、デジタル回路は電気を溜めたり抜いたりを繰り返しています。出力が0から1になり再び0にもどるということは、電源から器(容量)に電気(正確には電荷)を流し込み(出力が0から1)、その器に溜まった電気をグランド(GND)に放出している(出力が1から0)ということです。この1サイクルの間に電源からグランドに流れた電気(正確には電荷)は、器(容量)に溜まった電気に等しいので、平均電流はその器(容量)に溜まった電気を1サイクルの時間で割ったものになります。その平均的な電流と電圧の掛け算で消費電力が計算できます。充電と放電は間を置かず連続して起こるとして計算します。
容量に溜まる電荷Q=CV、充放電時間をTとすると平均電流I=Q/T =CV/T
よって消費電力P=VI=V x (CV/T)=CV2/T
1/2にスケーリングすると本文で述べたようにC、V、Tがそれぞれ1/2になるので
スケーリング後の消費電力P’=(C/2) x (V/2)2/(T/2)=(1/4) x (CV2/T)=(1/4) x P
したがって本文の「例えば1/2にスケーリングするとどうなる?」の節で述べたのと同じ1/4になります。面積も同様に1/4になりますので単位面積当たりの電力はスケーリングしても同じということになります。
なお一般的にはデジタル回路の消費電力は以下のように表されます。
P∝CV2f
ここでfは動作周波数です。周期をTとするとf=1/Tなので右辺はCV2/Tとなり上と同じ式になります。
2025年04月23日 更新
1.「デジタル回路はなぜ高速化するのか?」の節の「①デジタル回路とは」の内容を見直しました。
2.補足説明に「デジタル回路の消費電力とスケーリング」を追加しました。
※その他の記事はこちら:
シリーズ:半導体の微細化
第1回: 半導体の微細化 ムーアの法則とは
第2回: 半導体の微細化と半導体プロセス
第3回: 半導体の微細化と国際半導体技術ロードマップ
第4回: 半導体の微細化と半導体ビジネス
第5回: 半導体の微細化と半導体ビジネス その2
第6回: 半導体の微細化と半導体デバイス
第7回: 半導体の微細化 スケーリング則とは
第8回: 半導体の微細化 スケーリング則の限界
第9回: 半導体の微細化とアナログ回路
シリーズ:Siウェーハの大口径化
第10回: Siウェーハの大口径化 ~ありふれた物質Si(シリコン)が主役になるまで~
第11回: Siウェーハの大口径化(その2) ~Siウェーハができるまで~
第12回: Siウェーハの大口径化(その3) ~大口径化の理由と歴史~
シリーズ:半導体産業の水平分業化
第13回: 半導体産業の水平分業化とファブレスの躍進
第14回: 半導体産業の水平分業化の歴史~ファブレス半導体企業の誕生~
第15回: 半導体産業の水平分業化の歴史~ファウンドリの誕生~
第16回: 半導体産業の水平分業化 ~ファウンドリは下請けか?~
第17回: 半導体産業の水平分業化 ~製品別、国別の水平分業の実態(前編)~
第18回: 半導体産業の水平分業化 ~製品別、国別の水平分業の実態(後編:国別)~
第19回: 半導体産業の微細化と水平分業化(番外編)~先端ロジック半導体の起源と定義と種類~
第20回: 先端ロジック半導体の仲間たち ~CPU、GPU、MPU、MCU、SoCとは~
第21回: 半導体産業の微細化と水平分業化(番外編)~チップレットとは~






Comment